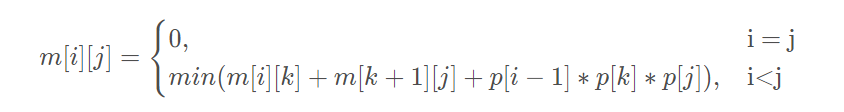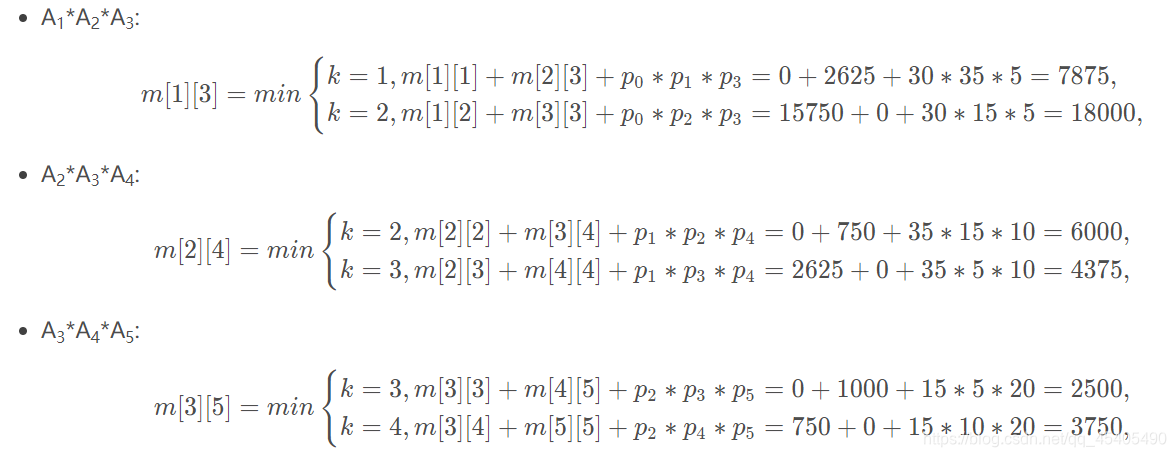河北大学程序设计训练营

题目描述：
矩阵的乘法定义如下：设A是m×p的矩阵，B是p×n的矩阵，则A与B的乘积为m×n的矩阵，记作C=AB，其中，矩阵C中的第i行第j列元素cij 可以表示为：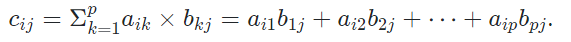
在这里插入图片描述
当多个矩阵相乘时，采用不同的计算顺序所需的乘法次数不相同。例如，A是50×10的矩阵，B是10×20的矩阵，C是20×5的矩阵， 计算ABC有两种方式：(AB)C和A(BC)，前一种需要15000次乘法计算，后一种则只需3500次。

设A1 ,A2 ,…,An 为矩阵序列，Ai 是阶为Pi−1 ∗Pi 的矩阵(1≤i≤n)。试确定矩阵的乘法顺序，使得计算A1 A2 …An 过程中元素相乘的总次数最少。

输入格式:
每个输入文件为一个测试用例，每个测试用例的第一行给出一个正整数(1≤n≤100)，表示一共有n个矩阵A1 ,A2 ,…,An ，第二行给出n+1个整数P0 ,P1 …Pn ，以空格分隔，其中1≤Pi ≤100(0≤i≤n)，第i个矩阵Ai 是阶为Pi−1 ∗Pi 的矩阵。

输出格式:
获得上述矩阵的乘积，所需的最少乘法次数。

输入样例:
在这里给出一组输入。例如：

5
30 35 15 5 10 20

输出样例:
在这里给出相应的输出。例如：

11875

思路过程：
(1) 矩阵 Ai*j与矩阵Bj*k相乘，所需乘法次数 = i* j*k,这点很容易理解

(2) 下面来分析最优解的情况：

  • 两个矩阵相乘，只有一个结果，所以不存在最优问题
  • 多个矩阵相乘，假设已经知道在第k个位置加括号会得到最优解，那么运问题变成两个子问题:（Ai Ai+1 …Ak)，(Ak+1Ak+2…Aj)​假设前者乘法次数为a，后者乘法次数为c，两者 相乘的乘法次数为b，所以，最优解 = a+b+c；

(3) 建立最优值递归式：

  • 用m[i][j]表示AiAi+1…Aj矩阵连乘的最优值，那么子问题（Ai Ai+1 …Ak)，(Ak+1Ak+2…Aj)对应的最优值为m[i][k],m[k+1][j],再加上矩阵（Ai Ai+1 …Ak)和矩阵(Ak+1Ak+2…Aj)的乘法次数就行。

  • 设矩阵Am的行数为pm，列数为qm,m=i,i+1,…，j，且矩阵可乘。（Ai Ai+1 …Ak)视为结果是一个pixqk矩阵，(Ak+1Ak+2…Aj)的结果是一个pk+1xqj矩阵，其中，qk = pk+1，两矩阵相乘的乘法次数是pi* pk+1*qj。

  • 矩阵连乘最优值递归式：
    当i=j时，只有一个矩阵，m[i][j] = 0;
    当i>j时，m[i][j] = min{ m[i][k] + m[k+1][j] + pipk+1qj},i≤k<j。

    如果用p[]来记录矩阵的行和列，第i个矩阵的行数存储在数组的第i-1位置，列数在数组的第i位置，那么pi* pk+1qj对应的数组元素相乘为p[i-1] p[k]*p[j],原递归式变为：
    在这里插入图片描述
    (4) 自底向上计算并记录最优值
    先求两个矩阵相乘的最优值，再求三个矩阵相乘的最优值，直到n个矩阵连乘的最优值。

(5) 图解
就本题来说，有5个矩阵，如图

矩阵 A1 A2 A3 A4 A5
规模 30*35 35*15 15*5 5*10 10*20

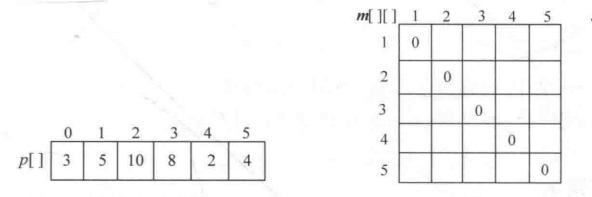
  • 初始化
    p[]记录行列值
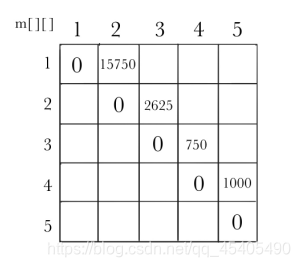
    m[][]记录最优值在这里插入图片描述

  • 计算2个矩阵相乘的最优值
    规模r = 2，根据递归式：m[i][j] = min{ m[i][k] + m[k+1][j] +p[i-1]* p[k]*p[j]},i≤k<j

    • A1*A2: k=1,m[1][2] = min{m[1][1] + m[2][2] + p[0]*p[1]*p[2]} = 15750

    • A2*A3: k=2,m[2][3] = min{m[2][2] + m[3][3] + p[1]*p[2]*p[3]} = 2625

    • A3*A4: k=3,m[3][4] = min{m[3][3] + m[4][4] + p[2]*p[3]*p[4]} = 750

    • A4*A5: k=4,m[4][5] = min{m[4][4] + m[5][5] + p[3]*p[4]*p[5]} = 1000
      计算完毕，

      在这里插入图片描述

  • 计算3个矩阵相乘的最优值
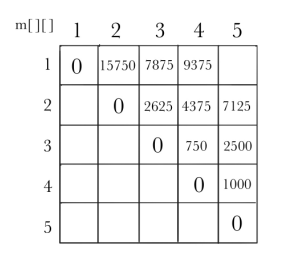
    在这里插入图片描述
    计算完毕,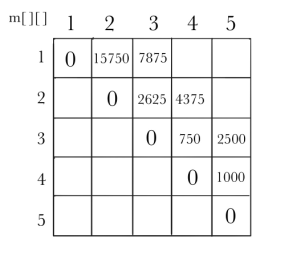

    ![在这里插入图片描述](https://img-blog.csdnimg.cn/20200811190136268.png)

  • 计算4个矩阵相乘的最优值
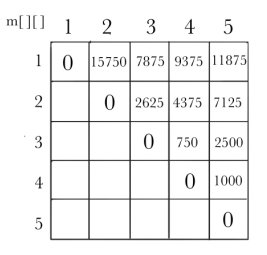
    在这里插入图片描述

  • 计算5个矩阵相乘的最优值
    在这里插入图片描述
    思路讲到这，现在来说说代码的鲁棒性:

就算法竞赛来讲，题目是人设计的，难免会出错。虽然比赛中途往往会修改这一错误，但在ACM/ICPC 等时间紧迫的比赛中，如果程序鲁棒性强，有时能在数据有瑕疵的情况下仍然给出正确的结果，这会节约大量不必要的时间浪费。

比如这道题，规定1≤n≤100，但是，n的实际输入值大于100，如果将MAX设置成105，结果如下，
在这里插入图片描述
段错误一般情况下就是数组太小，出现越界情况，所以就增大MAX吧。经测试，MAX到500就行，我猜是出题人少了个0，所以直接写了1005。

AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <bits/stdc++.h>

using namespace std;

const int MAX = 1005;
int p[MAX];
int m[MAX][MAX];
int n;

void  matrix()
{
    int i,j,r,k;
    memset(m,0,sizeof(m));
    for(r = 2; r<=n; r++)
    {
        for(i = 1; i<=n-r+1; i++)
        {
            j = i+r-1;
            m[i][j] = m[i+1][j]+p[i-1]*p[i]*p[j];
            for(k = i+1; k<j; k++)
            {
                int t = m[i][k] +m[k+1][j]+p[i-1]*p[k]*p[j];
                if(t<m[i][j])
                {
                    m[i][j] = t;
                }
            }
        }
    }
}

int main()
{
    cin>>n;
    //记录输入的数字,注意个数比n多1
    for(int i=0; i<n+1; i++)
        cin>>p[i];
    matrix();
    cout<<m[1][n];
    return 0;
}