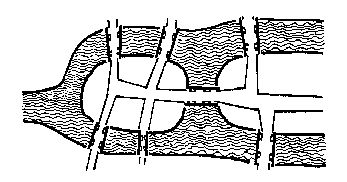
哥尼斯堡是位于普累格河上的一座城市，它包含两个岛屿及连接它们的七座桥，如下图所示。

img

可否走过这样的七座桥，而且每桥只走过一次？瑞士数学家欧拉(Leonhard Euler，1707—1783)最终解决了这个问题，并由此创立了拓扑学。

这个问题如今可以描述为判断欧拉回路是否存在的问题。欧拉回路是指不令笔离开纸面，可画过图中每条边仅一次，且可以回到起点的一条回路。现给定一个无向图，问是否存在欧拉回路？

输入格式:

输入第一行给出两个正整数，分别是节点数N (1≤N≤1000)和边数M；随后的M行对应M条边，每行给出一对正整数，分别是该条边直接连通的两个节点的编号（节点从1到N编号）。

输出格式:

若欧拉回路存在则输出1，否则输出0。

输入样例1:

1
2
3
4
5
6
7
8
9
10
11
6 10
1 2
2 3
3 1
4 5
5 6
6 4
1 4
1 6
3 4
3 6

输出样例1:

1
1

输入样例2:

1
2
3
4
5
6
7
8
9
5 8
1 2
1 3
2 3
2 4
2 5
5 3
5 4
3 4

输出样例2:

1
0

思路：

​ 判断一个图是否有欧拉回路，其充分必要条件为不存在度为奇数的点。

​ 同时此题还需判断图是否是连通状态的，所以要用一个并查集来判断

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 5;
int n,m,degree[N],f[N];
int Find(int x){
    if(f[x] == -1) return x;
    else    return f[x] = Find(f[x]);
}
int main() {
    cin >> n >> m;
    memset(f,-1,sizeof(f));
    for(int i = 0; i < m; ++i){
        int u,v;
        cin >> u >> v;
        //记录度数
        degree[u]++,degree[v]++;
        int fa = Find(u),fb = Find(v);
        if(fa != fb)    f[fb] = fa;
    }
    int father = Find(1);
    //如果所有结点的父亲不是同一个，则图不连通
    for(int i = 2; i <= n; ++i){
        if(father != Find(i)){
            puts("0");exit(0);
        }
    }
    //如果有奇数度的点，则不存在欧拉回路
    for(int i = 1; i <= n; ++i){
        if(degree[i] & 1){
            puts("0");exit(0);
        }
    }
    puts("1");
    return 0;
}